C++版ROS2のメッセージ型構造体にカスタムメモリアロケータを指定したい
この記事は, ROS2 Advent Calendar 2022 の12月16日分の記事です.
2022年12月16日時点のROS2エコシステムの現状を元に書いた記事ですので, 近い将来事情が変わっているかもしれません.
こんにちは, @sykwer です. 普段は自動運転システムに特化したOSやそのリアルタイム性についての研究開発をしています.
本記事は, C++版のROS2メッセージ型構造体に対して, カスタムメモリアロケータを指定することができるか検証するという内容になります.
ROS2公式ドキュメントに示される通り, publisherオブジェクト, subscriptionオブジェクト, executorオブジェクトなどに対してカスタムアロケータを渡すことができます (Implementing a custom memory allocator — ROS 2 Documentation: Humble documentation). しかし, rosidlによって生成されるROS2メッセージ型構造体のメモリ戦略を指定するためのカスタムメモリアロケータの渡し方はどこにも載っていません.
ROS2メッセージ型構造体にカスタムメモリアロケータを渡す方法が存在するか確かめるために, rosidlの中身や, rosidlによって自動生成されるコードの中身を調査します.
- カスタムメモリアロケータを指定するモチベ
- rosidlで生成されるROS2メッセージ型構造体の定義
- ナイーブなアロケータ指定と symbol lookup error
- C++のコンテナ型が抱える負債と多相アロケータ
- rosidl改造による多相アロケータの導入
- ROS2エコシステム全体の修正の必要性
- まとめ
カスタムメモリアロケータを指定するモチベ
C++においては, std::vectorやstd::mapなどのコンテナ型に対して, テンプレート引数でアロケータ型を指定することができます.
template<class T, class Allocator = std::allocator<T>> class vector; template<class Key, class T, class Compare = std::less<Key>, class Allocator = std::allocator<std::pair<const Key, T>>> class map;
このアロケータ型を明示的に指定しない場合, std::allocator<T> がデフォルトアロケータとして使用されます. 後の章で説明する通り, rosidlによって自動生成されるROS2メッセージ型構造体も同様で, アロケータには std::allocator<T> が使用されます.
C++におけるアロケータとは, C++ named requirements: Allocator - cppreference.com で説明される条件を満たしたクラスのことであり, ざっくり言うと allocate と deallocate をメソッドとして持つクラスです. std::allocator<T> は以下のように, allocate()呼び出しでは operator new() を, deallocate()呼び出しでは operator delete()を呼び出します.
namespace std { template <typename T> class allocator { public: using value_type = T; T* allocate(size_t n) { return ::operator new(n * sizeof(T)); } void deallocate(T *p, size_t n) { ::operator delete(p, n * sizeof(T)); } }; }
operator new() 等でメモリの確保をすると, brk(2) か mmap(2) どちらかのシステムコールが呼ばれることがあります. brk(2) は既存のheap領域にあたる vm_area_struct のサイズを拡張するシステムコールであり, mmap(2) は新規に vm_area_struct を作成するシステムコールです.
※ vm_area_structについて
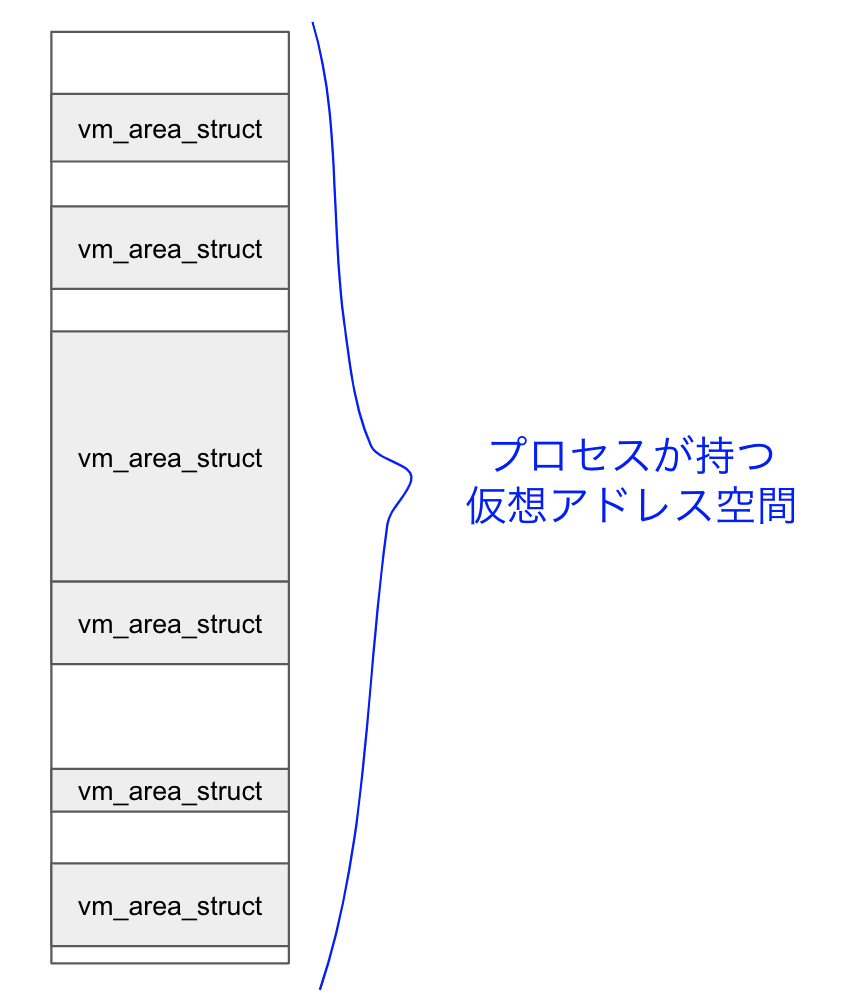
以下の図のように, プロセスが持つ仮想アドレス空間は, vm_area_struct のリストとして管理されています. ユーザプログラムはこの vm_area_struct が示すアドレス範囲にのみアクセスすることができ, この範囲外にアクセスする命令を発行すると, Segmentation Fault が発生します.
この vm_area_struct のどれかが, いわゆる text領域, data領域, stack領域, heap領域 とか呼ばれたりするものです. mmapシステムコールによって, ユーザプログラムから自由に vm_area_structを作成することができます.
プロセスが作成された当初は一定のサイズの heap領域 (1MB?) が確保されています (下図左).
この領域はユーザ空間のmallocランタイムによって管理されています. mallocランタイムはこの領域をmemory chunkの集合として管理し, ユーザプログラムからの割り当て要求にしたがって, memory chunkを渡します. mallocランタイムの実装に依存しますが, memory chunkはくっついたり分割されたりして, 頭良くこの領域を使おうとします.
ユーザプログラムからメモリ割り当て要求が続くと, heap領域が足りなくなってしまいます. 足りなくなるとmallocランタイムは brk(2) を発行します. brk(2) でheap領域を拡張することによって, mallocランタイムは, 使用することができる仮想アドレス空間リソースを追加することができます (下図真ん中).
あるサイズより小さな malloc(size) 呼び出しの場合は brk(2) によるheap領域拡張を引き起こしますが, あるサイズより大きなメモリ割り当て要求をすると mmap(2) によってmallocランタイムが使用することができる仮想アドレス範囲リソースを追加しようとします (下図右)
さて, このようにmallocランタイムでは仮想アドレス空間リソースの確保が行われますが, 注意しなくてはならないことは, 仮想アドレス空間リソースが最初に確保された時点では, 対応するページテーブルのエントリに物理ページ番号が挿入されておらず, first touchでソフトページフォルトが発生するという点です.
このソフトページフォルトが実行時間に大きなスパイクを発生させるため, リアルタイムシステムにとっては致命的となります. 例として GitHub - ros2/common_interfaces: A set of packages which contain common interface files (.msg and .srv). で提供されている PointCloud2 型を挙げます. 例えば, 出力メッセージのメモリ領域初期化のコードは以下となります.
auto output_msg = std::make_unique<PointCloud2>(); output_msg->data.resize(POINTS_DATA_SIZE); // fill output_msg publisher_->publish(std::move(output_msg);
この POINTS_DATA_SIZE が10MB強であるときの, output_msg->data.resize() にかかるターンアラウンドタイムの時系列推移 (横軸: 呼び出し回数インデックス, 縦軸: ターンアラウンドタイム (us)) とそのヒストグラムは以下のようになります. スパイクが多数発生していることが分かります.

このスパイクが発生している箇所がソフトページフォルト由来であることを明らかにするために, output_msg->resize() の処理区間における Performance Counterの minor-faults の数を横軸に, ターンアラウンドタイムを縦軸にプロットして散布図を作りました. すると以下のように, 綺麗な比例関係にあることが分かり, ソフトページフォルトがスパイクの原因になっていることがはっきりしました. ソフトページフォルトが発生したりしなかったりするのは, operator delete()に伴って munmap(2) で仮想アドレス空間リソースを解放するかどうかは, mallocランタイムの実装依存によるタイミングに依存しているからです.

このようなソフトページフォルトが発生することを防ぐには, あらかじめfirst touchした領域からのみメモリ割り当てをするようなカスタムメモリアロケータが必要になります.
また, リアルタイムシステム向けに推奨されたメモリ割り当てアルゴリズムというのも存在しており, 組み込み環境でリアルタイムシステムを構築するためには, 全てのheap割り当てにカスタムメモリアロケータを用意するのは必須と言えるでしょう.
rosidlで生成されるROS2メッセージ型構造体の定義
さて, ROS2メッセージ型構造体にカスタムメモリアロケータを指定する必要性が分かったので, まずカスタムメモリアロケータを適用する先の構造体の定義を見ていくこととします. 今回は先ほどの例にも出した sensor_msgs パッケージの PointCloud2 メッセージ型を例とします.
rosidlは, .msg ファイルに独自フォーマットで記述されたROS2メッセージのフィールド情報を元に, 様々なヘッダファイルやソースファイルを自動生成します. その中でも, オリジナルROS2メッセージの構造体を定義した .hpp ファイルは install/パッケージ名/include/パッケージ名/msg/detail/型名__struct.hpp に生成されます.
sensor_msgs パッケージは rosdep でインストールすると, もちろん /opt/ros/{ros2 version name}/ 以下にインストールされています. sensor_msgs::msg::PointCloud2 の構造体を定義したヘッダファイルは, /opt/ros/{ros2 version name}/include/sensor_msgs/msg/detail/point_cloud2__struct.hpp に配置されているので, 見に行ってみましょう. 大部分を省略したコードを以下に示します.
namespace sensor_msgs { namespace msg { template<class ContainerAllocator> struct PointCloud2_ { explicit PointCloud2_( rosidl_runtime_cpp::MessageInitialization _init = rosidl_runtime_cpp::MessageInitialization::ALL ) { } explicit PointCloud2_( const ContainerAllocator &_alloc, rosidl_runtime_cpp::MessageInitialization _init = rosidl_runtime_cpp::MessageInitialization::ALL, ) { } }; using PointCloud2 = sensor_msgs::msg::PointCloud2_<std::allocator<void>>; } }
このように, PointCloud2 というのは template<class ContainerAllocator> struct PointCloud2_ に対してアロケータを std::allocator<void> に指定したものであるということが分かります.
ナイーブなアロケータ指定と symbol lookup error
前章の内容を踏まえると, ROS2アプリケーション側から以下のように, カスタムメモリアロケータをROS2メッセージ構造体に対して設定できそうです.
template<typename T> class MyAllocator { ... }; MyAllocator<void> my_allocator; auto output_msg = std::make_unique<sensor_msgs::msg::PointCloud2_<MyAllocator<void>>(my_allocator); ...
しかし, この一見うまくいくナイーブなアプローチでは, 実行時の symbol lookup error: undefined symbol というエラーメッセージと共に落ちてしまいます.
具体的には, rclcpp 内のヘッダファイルから呼ばれている以下の関数で symbol lookup error: undefined symbol が発生していました (ソースコード該当箇所:rclcpp/rclcpp/include/rclcpp/get_message_type_support_handle.hpp at 33dae5d679751b603205008fcb31755986bcee1c · ros2/rclcpp · GitHub ). この関数は例えば rclcpp::Node::create_publisher() の呼び出しに従って呼ばれます.
namespace rclcpp { get_message_type_support_handle() { auto handle = rosidl_typesupport_cpp::get_message_type_support_handle<MessageT>(); if (!handle) { throw std::runtime_error("Type support handle unexpectedly nullptr"); } return *handle; } }
この rosidl_typesupport_cpp::get_message_type_support_handle という関数は, ヘッダファイルrosidl/rosidl_runtime_cpp/include/rosidl_runtime_cpp/message_type_support_decl.hpp at galactic · ros2/rosidl · GitHub で以下のように宣言されています.
template<typename T> const rosidl_message_type_support_t * get_message_type_support_handle();
今回の場合は, Tにsensor_msgs::msg::PointCloud2_<MyAllocator<void>> が渡されて, ROS2アプリケーション側バイナリのシンボルテーブルには, カスタムアロケータ版メッセージ型でインスタンス化された関数名シンボルが入っていることが nm -D で確認できます.
結論から述べると, 今回生じた問題の理由は, rosidl_typesupport_cpp::get_message_type_support_handle という関数の実装側に, その「カスタムアロケータ版メッセージ型でインスタンス化された関数名シンボル」が存在していないことです.
rosidl_typesupport_cpp::get_message_type_support_handle という関数の実装は, rosidl が .msg ファイルから自動生成したソースファイルの中に含まれています. PointCloud2 の場合は /opt/ros/{ros2 version name}/include/sensor_msgs/msg/detail/point_cloud2__type_support.cpp に該当ソースファイルが配置されていました. そこには以下のように rosidl_typesupport_cpp::get_message_type_support_handle という関数が定義されていることが確認できました.
#include <sensor_msgs/msg/detail/point_cloud2__struct.hpp> #include <rosidl_typesupport_introspection_cpp/message_type_support_decl.hpp> template<> ROSIDL_TYPESUPPORT_INTROSPECTION_CPP_PUBLIC const rosidl_message_type_support_t * get_message_type_support_handle<sensor_msgs::msg::PointCloud2>() { return &::sensor_msgs::msg::rosidl_typesupport_introspection_cpp::PointCloud2_message_type_support_handle; }
get_message_type_support_handleのテンプレート引数の部分に sensor_msgs::msg::PointCloud2と書かれています. これはすなわち sensor_msgs::msg::PointCloud2_<std::allocator<void>> ということであるので, メッセージ型のアロケータが std::allocator<void> の場合に対してのみ, この関数は実装を用意しているということになります. もちろん MyAllocator<void> に対する実装は存在しないので, symbol lookup error: undefined symbol になるというわけです.
ちなみに, このアロケータを std::allocator<void> とベタ書きしている empy テンプレートファイルの箇所は rosidl/rosidl_typesupport_introspection_cpp/resource/msg__type_support.cpp.em at b8381d955a111cdf8a52a0f1891cc55de5f19db1 · ros2/rosidl · GitHub です.
C++のコンテナ型が抱える負債と多相アロケータ
今回発生した問題の根本的な原因は, C++のコンテナ型にアロケータ型が含まれてしまっているという点です. そもそもアロケータの違い (メモリ割り当て戦略の違い) がコンテナ型に現れるべきではありません.
この議題に関しては, C++17から導入された 多相アロケータが解決を図ろうとしています. 多相アロケータは std::pmr 名前空間に実装されています. ドキュメントは std::pmr::polymorphic_allocator - cppreference.com です.
C++の多相アロケータは, いままでのアロケータ型を含んでしまっているコンテナ型との連続性を保ちつつ, アロケータを差し替えても, コンテナ型に変化がないようにする工夫をしました. すなわち, コンテナ型に常に同じアロケータ型 (std::pmr::polymorphic_allocator) を渡し, メモリ割り当て戦略の実装は外部のオブジェクト(std::pmr::memory_resource) に任せて, std::pmr::polymorphic_allocator オブジェクトは std::pmr::memory_resource オブジェクトへのポインタを持つだけという方法です (Strategy Patternですね).
これならば, メモリ割り当て戦略である std::pmr::memory_resource オブジェクトの差し替えをおこなったとしても, コンテナ型 (例えば std::vector<int, std::pmr::polymorphic_allocator>) は変化することはありません. ただ唯一の欠点としては, 多相アロケータ型を含むコンテナ型同士でメモリ割り当て戦略が型に現れないというだけで, 既存のメモリアロケータ (例えば std::allocator) を含むコンテナ型とは型の違いが出てしまうという点です. つまり, 明日朝起きたら全てのコンテナ型のアロケータ型が std::pmr::polymorphic_allocator に置き換わっていると人類が幸せになれるということです.
次章では, rosidl を中心としたROS2メッセージのエコシステムに, 多相アロケータを導入することによって, ROS2メッセージ構造体にカスタムアロケータを渡せるようにならないかを検証します.
rosidl改造による多相アロケータの導入
ROS2メッセージ構造体のアロケータ型として, 多相アロケータを導入することが可能であるかを検証します. その手順は以下の通りとなります.
セルフビルドのROS2環境を作る
ROS2メッセージ構造体の定義にて,
using PointCloud2 = sensor_msgs::msg::PointCloud2_<std::allocator<void>>;というようになっている箇所がusing PointCloud2 = sensor_msgs::msg::PointCloud2_<std::pmr::polymorphic_allocator<void>>;となるように, ros2/rosidl repositoryで管理しているempyテンプレートファイルを書き換えて, ビルドし直す.全てのROS2メッセージ構造体のアロケータが
std;;pmr::polymorphic_allocator<void>に変更されたら, ROS2環境全体をビルドしなおし, ビルドが通らない箇所を地道に直していく (修正箇所の規模を把握する).
include/sensor_msgs/msg/detail/point_cloud2__struct.hpp のような, ROS2メッセージ構造体を定義するヘッダファイル等は, (galacticの場合は) common_interfaces/sensor_msgs/CMakeLists.txt at galactic · ros2/common_interfaces · GitHub のように rosidl_generate_interfaces という rosidl で定義されたCMakeマクロをトリガーとして生成されます. 生成元となるファイルは, ros2/rosidl repository内にて .em という拡張子の empyテンプレートファイルとして管理されています.
.em ファイルで, using PointCloud2 = sensor_msgs::msg::PointCloud2_<std::allocator<void>>; のようなコードを生成する箇所は rosidl/rosidl_generator_cpp/resource/msg__struct.hpp.em at galactic · ros2/rosidl · GitHub であるので, ここの std::allocator<void> を std::pmr::polymorphic_allocator<void> に書き換えて, ファイルの冒頭に #include <memory_resource> と追記し, ROS2環境全体をビルドし直せばよいです.
※ 2022/12/16現在, ROS2エコシステム全体はC++14でビルドされるように各 CMakeLists.txt が設定されており, C++17からのfeatureである std::pmr 名前空間の機能を使うことができません. とりあえず std::experimental::pmr に生えているAPIを使えばC++14でも多相アロケータを使用することができるのでそちらで実験します.
ROS2エコシステム全体の修正の必要性
rosidl/rosidl_generator_cpp/resource/msg__struct.hpp.em にて std::allocator<void> を std::pmr::polymorphic_allocator<void> に書き換えて, ROS2エコシステム全体をビルドしなおすと, 様々な種類のビルドエラーが生じました.
ビルドエラーの原因としては, ROS2エコシステム各repositoryに記述されているソースコード中で, std::allocator 型を含むコンテナ型と, ROS2メッセージ型の内部のコンテナプロパティ (std::pmr::polymorphic_allocator 型を含む) 間で型の不整合が起きていることが中心でした.
例えば, common_interfaces/sensor_msgs/include/sensor_msgs/impl/point_cloud2_iterator.hpp at galactic · ros2/common_interfaces · GitHub では以下のように文字列比較をしているために型の不整合が発生しています.
while ((field_iter != field_end) && (field_iter->name != field_name)) {
...
}
libstatistics_collector/src/libstatistics_collector/collector/generate_statistics_message.cpp at galactic · ros-tooling/libstatistics_collector · GitHubのように, 文字列代入を行おうとしている箇所でも型の不整合が起きます.
msg.metrics_source = metric_name;
rosidl_typesupport_fastrtps/rosidl_typesupport_fastrtps_cpp/resource/msg__type_support.cpp.em at galactic · ros2/rosidl_typesupport_fastrtps · GitHub のように, std::wstring ( std::basic_string<wchar_t, std::char_traits<wchar_t>, std::allocator<wchar_t>) と .em ファイルの中にベタ書きしてしまっている事例も見受けられます.
他にもたくさんの型不整合が発生する箇所があります. つまり, 多相アロケータを導入するアプローチを成功させようとすると, ROS2エコシステムの膨大なrepository群に一つ一つ修正のPRを出さなくてはならず, また今後のコミュニティの開発にてこのような型不整合を引き起こすコードが入り込まないように監視する必要が出てきてしまいます.
まとめ
2022/12/16現在から観測して, C++ ROS2のメッセージ型構造体にカスタムメモリアロケータを指定するのはかなりの困難を伴うことになります. 取れる選択肢としては,
ROS2エコシステム全体 (というか全世界) の
std::vectorやstd::stringのようなコンテナ型が, 明日朝起きたら全てstd::pmr::vectorやstd::pmr::stringに書き変わっている (無理)ROS2エコシステム全体の
std::allocator<void>となっている由来のビルドエラー箇所を1つずつ修正してPRを出す (しんどすぎる)ROS2エコシステムを脱出する (???)
ただ, メッセージ型構造体に直接カスタムメモリアロケータを指定するという綺麗なアプローチを諦めて, もう全てのheapメモリ割り当て要求を LD_PRELOAD で引っ掛けて, まるごとカスタムメモリアロケータを適用してしまうという多少汚いアプローチを取ってしまうのが丸いかもしれません.
→ つくりました https://github.com/tier4/heaphook
[組み込みOS - kozos] スイッチを押してからOSがコマンド応答するまでを追う
これは 自作OS Advent Calendar 2018 - Adventar 23日目の記事です
0. はじめに
@kozossakai さんが開発された kozos という, H8/3069Fの上で動く組み込みOSをベースにして, 色々改造した内容をアドベントカレンダー向けに書きたかったのですが, 時間がとれなかったので内容を急遽変更し, 「リセットスイッチを押してからOSがコマンドに応答して出力をコンソールに返すまで」の処理を順番に追っていくという記事にすることにしました. 論文とかではないので新規性は気にしません.

ここで追っていくコードは, 12ステップで作る組込みOS自作入門 で完成したコードを自分の扱いやすいように少しいじったものになります. 以下のrepoでv0.1.0として公開されています.
1. H8/3069Fについて
この組み込みOSが動作するマイクロコンピュータである, H8/3069Fに関する簡単な前提知識を書いておきます.
- H8/3069Fは, H8/300H CPUを核にした, シングルチップマイクロコンピュータ
- 内部32ビット構成で, 16ビット × 16本の汎用レジスタを持つ 16MBのリニアなアドレス空間を扱うことができる
- 今回用いる周辺機能は, ROM, RAM, Serial Communication Interface(シリアル通信を担う周辺デバイス. 以後SCI)
- 512KBのフラッシュメモリ(ROM)と, 16KBのRAMが内蔵されている
- SCIは3チャネル存在するが, 今回は1チャネルしか用いない
2. 大まかな流れ
まず, bootloaderの実行バイナリをあらかじめROMに焼き込んでおきます(この焼き込み回数に上限があるので, bootloaderはあまり変更ができません. 手順は README参照). OSのコードは, bootloaderのコードの中からダウンロードされます.
リセットスイッチを押すとまずbootloaderが起動し, bootloaderはホストマシンからOSの実行可能ファイルをシリアル経由でダウンロードしてRAM上に展開し, そしてbootloaderがOSを起動するという流れになります.
さっそく, リセットスイッチを押すとまず何が起こるのか..から始めたいところですが, メモリマッピングが分からないと処理の内容が分かりにくいと思うので, bootloaderのメモリマッピングを見てから, bootloaderの処理を見ていくことにします.
3. bootloaderのメモリマッピング
アドレス割り当てを知るには, bootloaderのリンカスクリプトを見ればいいのですが図にしておきます. 前章で説明したように, H8/3069Fには512KBのフラッシュROMと16KBのRAMが内蔵されており, 図のようにアドレスがマッピングされます.
(下の図には表記されていませんが, 0xffff20 ~ 0xffffe9 には内蔵I/Oレジスタがマッピングされています)

次に定義された各領域にどのようなデータが割り当てられるのかを知るために, セクションの定義を見てみます. セクションの定義は以下のように書かれています(長いのでソースのコメントで解説を書きます).
SECTIONS { /* vectorsの領域には, vector.oというオブジェクトファイルのdata領域の */ /* 情報が書き込まれます (このvectorとは割り込みベクタに当たります) */ .vectors : { ../../bin/bootload/obj/vector.o(.data) } > vectors /* text領域(実行可能コード)はromに書き込まれます */ .text : { _text_start = . ; *(.text) _etext = . ; } > rom /* read only data はromに書き込まれます */ .rodata : { _rodata_start = . ; *(.strings) *(.rodata) *(.rodata.*) _erodata = . ; } > rom .softvec : { _softvec = .; } > softvec .buffer : { _buffer_start = . ; } > buffer /* data領域とbss領域においては, 変数の初期値はROM上に焼きこまれ, */ /* プログラムがdata/bss領域の変数を見にいくときは, RAM上のアドレスを見にいくようになっています. */ /* これは, 静的変数を実行中に書き換えられるようにするための処置であり, */ /* リンカスクリプトでは, 以下のように特別な記法がなされる */ /* (後々, ROM上の初期値を, RAM上にコピーする処理が行われるので, このようなことが可能になります) */ .data : { _data_start = . ; *(.data) _edata = . ; } > data AT> rom .bss : { _bss_start = . ; *(.bss) *(COMMON) _ebss = . ; } > data AT> rom . = ALIGN(4); _end = . ; .bootstack : { _bootstack = .; } > bootstack .intrstack : { _intrstack = .; } > intrstack }
また, 後々プログラム中からアドレスを取得するために, 以下のようなラベルが然るべきアドレスに対して設定されています.
text_start,etext: text領域の開始と終了rodata_start: read only dataの領域の開始と終了softvec: ソフトウェア割り込みベクタ(実際の割り込みハンドラへのポインタ. RAM上に置かれるので実行時に変更可) のアドレスbuffer_start: OSの実行可能ファイルがダウンロードされるときのバッファ領域の開始data_start,edata: data領域の開始と終了bss_start,ebss: bss領域の開始と終了bootstack: bootloaderの処理のスタックはこのアドレスから積まれるintrstack: 割り込みハンドラの処理のスタックはこのアドレスから積まれる
bootloaderの処理で使用したスタックが, 後々割り込みハンドリングで使用されるスタックで上書きされてしまいますが, bootloaderのスタックを保存する必要はないので問題ありません.
4. Bootloader
それではリセットボタンを押してみましょう.
4.1. リセットボタンを押してからスタートアップまで

リセットスイッチを押すと, まず割り込みベクタの0番目を見にいき, そこに格納されているアドレスにプログラムカウンタを書き換えて, 実行を開始します.
割り込みベクタの定義は bootload/vector.c に書かれています.
割り込みベクタとは, 周辺機器やシステムコールなどで割り込みが発生したときに, 要因に応じた場所の割り込みベクタ(下記のstartとかintr_serintr とか)を見て, そのアドレスに飛ぶというものでした. (つまり, 割り込みベクタ中の関数ポインタは, 割り込みハンドラのアドレスであると言い換えられる)
void (*vectors[])(void) = { start, NULL, NULL, NULL, NULL, NULL, NULL, NULL, intr_syscall, intr_softerr, intr_softerr, intr_softerr, // trap interrupt vectors NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, intr_serintr, intr_serintr, intr_serintr, intr_serintr, // SCI0 interrupt vectors intr_serintr, intr_serintr, intr_serintr, intr_serintr, // SCI1 interrupt vectors intr_serintr, intr_serintr, intr_serintr, intr_serintr, // SCI2 interrupt vectors };
前章より, この配列は 0x000000 ~ 0x0000ff の領域に書き込まれているのでした. 割り込みベクタの0番目は start という関数へのポインタです. つまり, リセットスイッチを押すと, start という関数から処理が始まります.
start は bootload/asm/startup.S に定義されています.
_start: mov.l #_bootstack,sp jsr @_main
スタックポインタに #_bootstack というアドレスを設定したのち, main という関数へのポインタにプログラムカウンタを書き換えています. #_bootstack は前章で見たリンカスクリプトで定義されていたラベルで, この先の処理では, このアドレスからスタックが積まれます. また, sp は er7 のエイリアスであり, er7 で表されるレジスタに現在のスタックポインタが保持されます.
4.2. main関数 - 初期化
main は bootload/main.c に定義されています(現在の説明でみる必要のないソースは省略 することにします).
static int init(void) { extern int erodata, data_start, edata, bss_start, ebss; // defined in linker script // グローバル変数の初期化(=> 下記 説明⑵) memcpy(&data_start, &erodata, (long) &edata - (long) &data_start); memset(&bss_start, 0, (long) &ebss - (long) &bss_start); // ソフトウェア割り込みベクタの初期化(=> 下記 説明⑶) softvec_init(); // 今回使用するSerial Communication Interfaceの初期化(=> 下記 説明⑷) serial_init(SERIAL_DEFAULT_DEVICE); } int main(void) { /* 省略 */ // 割り込みを禁止 (=> 下記 説明⑴) INTR_DISABLE; init(); /* 省略 */ }
説明⑴
まず, ブートロード中に割り込みが入ると非常に困るので INTR_DISABLE マクロで割り込みを無効にします.
INTR_DISABLE は bootload/interrupt.h で定義されています.
#define INTR_DISABLE asm volatile ("orc.b #0xc0, ccr")
INTR_DISABLEは, ccr というレジスタに対して or 演算で 0xc0 を足しこむインラインアセンブラであると分かります. ccr は1バイトのレジスタで, 最上位ビットを1にすることで割り込みが無効になります.
さて, init 関数の中では以下の説明⑵ ~ ⑷に解説される処理を行なっています. (なお, memcpy などのライブラリ関数は bootload/lib.c に定義されています)
説明⑵
ROM上のdata領域のデータを, RAM上のdata領域にコピーしています. これは, 前章で見たリンカスクリプトの解説のとおり, 「data領域とbss領域においては, 変数の初期値はROM上に焼きこまれ,プログラムがdata/bss領域の変数を見にいくときは, RAM上のアドレスを見にいくようになっている」ために必要な処理です.
また, RAM上のbss領域を初期化(ゼロクリア)しています. 初期値がゼロ値と決まっているので, memsetでゼロクリアしているだけです.
説明⑶
ソフトウェア割り込みベクタを初期化(ゼロクリア)しています (softvec_init). 現在はゼロクリアされた状態ですが, OS側から実行時に, 割り込みハンドリングの実際の処理を行う関数のポインタがここには設定されます.
説明⑷
今回使用するSCIのレジスタに初期値をセットしています(serial_init). serial_initの実際のコードとH8/3069Fの仕様書を読めば何をしているか理解できます.
4.3. main関数 - ホストPCからOS実行可能ファイルをダウンロード
さて, main 関数の続きを見ていきます.
int main(void) { static char buf[16]; // buffer for command from host PC static long size = -1; static unsigned char *loadbuf = NULL; // buffer for os binary image extern int buffer_start; // defined in linker script /* 省略 */ puts("kzload (kozos boot loader) started \n"); while (1) { puts("kzload> "); gets(buf); if (!strcmp(buf, "load")) { loadbuf = (char *) (&buffer_start); size = xmodem_recv(loadbuf); wait(); // 3*10^5 回のbusy waitをしているだけです if (size < 0) { puts("\nXMODEM receive error\n"); } else { puts("\nXMODEM receive succeeded!\n"); } } /* 省略 */ } /* 省略 */ }
まず, puts() は内部で serial_send_byte() を繰り返し呼ぶことにより, SCIの特定のレジスタを操作して, シリアル経由でホストPCに文字を送信しています(送信可能かどうかの判定はbusy loopでSCIの特定のレジスタを見張っています).
シリアル経由で, ホストPCのコンソールにbootloaderの開始メッセージとプロンプトが表示されました.

ここでコマンドを入力した上で enterを押して送信すると, gets()が繰り返しserial_recv_byte()を呼び出すことで, シリアル経由で送られてきた文字を, SCIの特定のレジスタから取得します(受信があるかどうかの判定はbusy loopでSCIの特定のレジスタを見張っています).
さて, 上記の main の中の処理は, コマンドとしてload を受け取った場合にあたります.
リンカスクリプトで定義された buffer_startが指す, buffer領域の始まりのアドレスを xmodem_recv() という関数に渡しています. この関数は, XMODEMというシリアル通信のプロトコルで, ホストPCからOSの実行形式ファイルを受け取り, buffer領域上に展開する処理をします.
XMODEMのプロトコルにより, OSの実行形式ファイルを受け取ってbuffer領域に格納する処理は bootload/xmodem.c に実装されているので, 興味のある人は読んでみてください.
ここまでで, 「OSの実行形式ファイルがbuffer領域上に展開された状態」が達成されました. あとは, 「buffer領域上の実行形式ファイルを, ベタバイナリとしてRAM上にロードして, OSのエントリポイントにプログラムカウンタを書き換えてジャンプする」を達成すればOSが起動できます!
4.4. main関数 - OS実行可能ファイルのロードとOS起動
さて, main の続きを見ていきます.
int main(void) { /* 省略 */ while (1) { puts("kzload> "); gets(buf); if (!strcmp(buf, "run")) { entry_point = elf_load(loadbuf); if (!entry_point) { puts("run command error"); } else { puts("start from entry point: "); putxval((unsigned long) entry_point, 0); puts("\n"); f = (void (*)(void)) entry_point; f(); // not returned here } } /* 省略 */ } /* 省略 */ }
上記の main の中の処理は, コマンドとしてrun を受け取った場合にあたります.
まず, buffer領域の先頭のアドレスをelf_load() に渡して呼び出しています.
先ほど load コマンドでbuffer領域に展開した実行形式ファイルは, メモリ上に展開するときのイメージそのままのバイナリではなく, ヘッダなどを含んだ特定のフォーマットで記述されています. elf_load はこのELFフォーマットで展開されている実行形式ファイルを解析して, ベタバイナリをRAM上に展開する役割を担います.
elf_loadは具体的に以下の処理をします.
- ELF形式である実行可能ファイルが適切なフォーマットであるか, H8/300で動作するにあたり正しい定数がセットされているかをチェックする.
- ELFファイルのセグメントの情報に基づいて,
memcpy,memsetによってロードを行う. これにより, OSのtext, data, bss領域などのベタバイナリのデータがRAM上に展開される.
さて, elf_load からは entry_point が返ってきます. これは, OSのエントリポイントのアドレスを指しています. OSのエントリポイントはOSのリンカスクリプト で定義されています.
ENTRY("_start")
定義によると start というラベルで表されるアドレスがOSのエントリポイントに指定されています.
ブートローダーの最後の仕事は, このentry_pointを関数ポインタとして呼び出すことです. これでOSのコードに処理は移ります.
start は os/asm/startup.s で定義されています.
_start: mov.l #_bootstack,sp jsr @_main
ブートローダのときと同様に, スタックポインタを設定したのち, OSのmain関数にジャンプしています.
int main(void) { INTR_DISABLE; puts("kozos boot succeed!\n"); /* 省略 */ }
main 関数ではまず割り込みを無効化した後に, puts 関数でOSの起動メッセージをシリアル経由でホストPCに送信しています.
OSの起動メッセージを無事確認することができました🎉
5. OS
さて, OSに処理が移ったところで, OSがマルチスレッドで動作し, コマンドに応答する様子を追っていきたいところですが, 記事が思ったより長くなってしまったので, OSのパートは別記事にしたいと思います...
深層強化学習アルゴリズムDDPGをしっかり理解する(3)
DDPGは、行動空間が連続である制御タスクを学習させる際に、選択肢に挙がる深層強化学習アルゴリズムの一つです.
アルゴリズムの幹となっているDeterministicPolicyGradientTheoremをしっかり理解するには、関連する論文を順に読んでいかなくてはならず、理解しにくいアルゴリズムだと思います.
web上にも、しっかり理解できるリソースが少なかったので、論文などにあたって記事にしてみました.
DeterministicPolicyGradientTheorem自体の解説は、以下の記事に書いてあるので、ちゃんと理解したい人は、下の記事から読んでみてください.
1) DPG Theoremのおさらい
前回の記事で解説したDPG-Theoremの導出済みのやつだけ確認しておきます.
これは、期待報酬和を最大化していくには、方策parameterの微小変化に対する、行動価値関数Qの勾配方向にparameterを更新すればよいことを示しています.
このアルゴリズムにおいては、方策関数と行動価値関数の2つを関数近似すればいいことが、上の式から分かります.
この2つの関数それぞれをDNNで表現した手法がDDPG(Deep Deterministic Policy Gradient)です.
2) DDPGのアルゴリズム
DDPGのアルゴリズムの全体像は以下のとおりです.

https://arxiv.org/pdf/1509.02971.pdf
着目すべき点は
- (DQNの論文での手法と同様に) ReplayBufferという、直近の軌道(s_t, a_t, r_t s_t+1)を多数保持しておき、そのリストの中からランダムにミニバッチをつくり、1stepの学習に利用している点. サンプル同士がi.i.d.であるという, 機械学習における前提条件を満たすために必要な手法.
- (DQNの論文での手法と同様に) Actorネットワークと, Criticネットワークそれぞれに対して, 学習ネットワークとは別に, targetネットワークを用意します. これは, Criticネットワークの教師データを算出するときに使う学習targetを安定させて, 学習を安定させることを目的としています.
- Criticネットワークは普通の教師あり学習で更新していき、ActorネットワークはDDPG-Theoremに基づき更新していきます.
- 学習中のエージェントのとるactionは, Actor学習ネットワークの出力にノイズを加えたものとなります. 学習するpolicyそのものと, 学習中のpolicy(=behavior policy)が異なるので, off-policyな強化学習に分類されます.
実際に動くコードで見ないと理解しにくいと思うので, 次の章で実装をします.
3) 実装
RLライブラリにはTensowflow, モデルの実験環境にはaigymを用いて実装をしていきます.
mainのコードを追うだけでも雰囲気がつかめるので, この記事にはmain.pyと, 特筆すべき部分のコードのみ載せておきます.
main.pyは以下のとおりです. 前章のアルゴリズムと比較するといいと思います. (間違いがあったらご指摘お願いします!)
このrepositoryで特に注意すべきは, DDPG-Theoremを使っている部分です. 数式で理解しにくい定理なので, コードで理解するのがいいと思います.
4) 参考文献
深層強化学習アルゴリズムDDPGをしっかり理解する(2)
この記事は、
これ↑の続きにあたるものです.
Deterministic policy gradient theoremの導出だけ知りたい! という人以外は、最初の記事から読むことをおすすめします.
2) DPGアルゴリズム
前回の記事では、確率的な方策(= とある状態sに対して行動aが確率的に決まる方策)をparameterizeし、平均報酬 or 割引報酬和が最大になるようにパラメータを更新していくアルゴリズムを導出し実装しました.
このようなアルゴリズムをSPG(stochastic policy gradient) algorithmと呼ぶことも紹介しました.
今回は、決定論的な方策(= とある状態sに対して一意に行動aが決まる方策)をparameterizeし、割引報酬和が最大になるようにパラメータを更新していくアルゴリズムを導出し、実装していきます.
このようなアルゴリズムをDPG(deterministic policy gradient) algorithmと呼びます.
かつては、決定論的な方策勾配は存在しないか、model-freeでない強化学習モデルでのみ存在すると考えられていました.
しかし、2014年のdeepmind社の論文により、決定論的な方策勾配が存在し、確率論的な方策勾配のアプローチよりも性能面で上回ることが示されました.
2.1) DPGアルゴリズムを使っていくモチベーション
この章では、SPGアルゴリズムに代わってDPGアルゴリズムを使っていくメリットについて書いていきます.
そのためにまずは、方策パラメータの更新則を示す、決定論的な勾配方策定理がどのような形をしているのかを見てみます.
以下の式が決定論的な勾配方策定理です. ただし、
- 今回、状態sと状態aには連続値を想定.
: 決定論的な方策. 状態sに対して行動aを一意に出力.
: 方策
のもとでの、状態sの割引分布(前回の記事を参照)
: 方策
のもとで、状態sで行動aをとったときの行動価値関数.
割引報酬和の勾配は、行動価値関数の勾配∇θQ(s, μ(s))に対して、状態sで期待値をとった形をしています.
さて、この形だと確率論的な方策勾配定理に対して何がうれしいのでしょうか.
前回の記事で考えた、確率論的な方策勾配定理(ただし、s, aが連続値バージョン)は以下のような形をしていました.
注目すべきは、何に対する期待値をとっているかです.
SPGは、状態空間と行動空間の2つに対して期待値をとっているのに対して、
DPGは、状態空間のみに対して期待値をとっています.
よってPGを推定するために必要なサンプル数が、SPGよりもDPGの方が少なくなり、計算量が小さくなるのです.
(特に、行動空間の次元数が大きいときにうれしい)
2.2) DPG theoremの導出
それでは、上述の確率論的な方策勾配定理を導出していきましょう.
2.3) DPGの直感的な理解
DPGは以下のような形をしていることが導かれました. 方策勾配は、行動価値関数の勾配の期待値というシンプルな形をしています.
2.4) DPGによる強化学習の特徴
DPGにおけるtarget-policyは、決定論的な方策なので、この方策をそのまま探索における方策に用いてしまうと、十分な探索を行うことができません.
そこで十分な探索を保証するために、学習対象となるtarget-policyとは別に、学習中の探索にもちいるbehavior-policyを用いなくてはなりません.
いわゆるoff-policyな強化学習です.
また、決定論的方策と行動価値関数との2つを関数近似し最適化していくので、いわゆるActor-Criticアルゴリズムに分類されます.
2.5) 実装
前回のSPGと同様に実装例を載せようと思いましたが、次回の記事で解説するDDPGは、DPGアルゴリズムに深いニューラルネットワークを導入したものであり、どちらもDPG theoremに基づくアルゴリズムなので、実装例は次回の記事に委ねることにしました.2.6) 参考文献
- これからの強化学習, 2016/10/31
- Deterministic Policy Gradient Algorithms, 2014/6/21
深層強化学習アルゴリズムDDPGをしっかり理解する(1)
- Stochastic Policy Gradient method
- Deterministic Policy Gradient method
- Deep Deterministic Policy Gradient method
1) SPGアルゴリズム
方策勾配に基づくアルゴリズムでは、「現在のtarget-policy(= 最適化の対象となる方策)にしたがってagentが行動しつづけたときの期待報酬 」を目的関数とします. つまり、target-policyのパラメータ
を更新しつづけた結果、期待報酬
が最大になることを目指します.
1.1) 2通りの期待報酬Jの表し方
1.1.1) 平均報酬でJを定義した場合
行動価値関数は
状態sに関する関数は、
(平均報酬でJを定義した場合のd(s)は、sの定常分布を表しています. つまり、確率分布を表す量となっています)
1.1.2) 割引報酬和でJを定義した場合
1.2) 勾配方策定理の導出
1.2.1平均報酬でJを定義した場合
1.2.2) 割引報酬和でJを定義した場合
1.3) 勾配の近似
1.4) 実装
- 10エピソードに渡って
の和をとったのち、その勾配方向に
を更新している.
- パラメータ
の更新にはRMSProp(直近で大きく更新した方向には、更新量が小さくなるようにする手法)を用いている.
といったアルゴリズムになっています.
入力データには前処理をした画像のraw-pixelを用いていますが、畳み込みニューラルネットワークではなく、通常のニューラルネットワークを用いています. 畳み込みニューラルネットワークを用いるとさらに性能が良くなるはずです.
1.5) 行動価値の推定
方策勾配の式をみてみると、勾配を求めるためには未知の行動価値関数を評価しなくてはならないことがわかります.
もっとも簡単な近似として知られているのが、を即時報酬
に置き換えてしまうアプローチです. この近似によるアルゴリズムをREINFORCEアルゴリズム[Williams, 1992]とよびます. これはちょっと荒すぎる近似であり、あまりいい性能もでないことから、大きな注目は浴びませんでした.
やはりもっとも妥当はアプローチは、行動価値関数も関数近似し、そのパラメータを最適化するアプローチでしょう.
このように、方策と行動価値関数とをモデル化し、そのモデルたちを更新し続けることで報酬和の期待値を最大化しようとするアプローチを、Actor-Criticアルゴリズムとよびます.
Actorという名前は、方策がagentの行動を決定しようとする主体であることに由来し、
Criticという名前は、方策勾配定理の中において、行動価値関数は方策モデルを評価しようとする批判者とみなせることに由来します.
さて、状態空間や行動空間が離散である場合は、行動価値関数をルックアップテーブルで保持して、行動価値関数を推定していくことが可能です.
しかし、状態空間や行動空間が連続である場合は、そのようなアプローチが困難なので、行動価値関数をパラメタライズされた関数で近似する必要があります.
このとき、以下のように行動価値関数をパラメタライズすると、バイアスのない推定ができることがわかっています[Sutton et al., 1999].
where
ほかにも、方策に確率的なものを想定したActor-Criticアルゴリズムによる、強化学習の手法がありますが、この記事シリーズの目的から外れてしまうので、紹介は省略します.
1.6) 参考文献
- Policy Gradient Methods for Reinforcment Learning with Function Approximation, 1999 https://papers.nips.cc/paper/1713-policy-gradient-methods-for-reinforcement-learning-with-function-approximation.pdf
- Deep deterministic policy gradients in TensorFlow, 2016/8/21 http://pemami4911.github.io/blog/2016/08/21/ddpg-rl.html
- これからの強化学習, 2016/10/31
- nishio/reinforcement_learning https://github.com/nishio/reinforcement_learning
次の記事では、Deterministic Policy Gradient methodについて書いていきます.
Hello Hatena Blog
@sykwerです. 人生初ブログです.
次の春で大学3年生になります. 無事に進級ができていれば東京大学の工学部に進めます. ソフトウェアエンジニアです.
このブログでは、ソフトウェアエンジニアリングに関連することを中心に書いていきたいと思っています.
4月から3年生ですが、大学は4年目です.
大学の2年目で休学してました. そのときwebベンチャーで1年くらいインターンしていたのですが、それをきっかけにエンジニアリングの世界に出会うことができました.
その会社では、railsでのサーバーサイド開発、reactでのフロントエンド開発、AWS周りの管理など、広く浅く(?) web開発周りの仕事をさせてもらいました. 仕事と呼べるほどのパフォーマンスではありませんでしたが.
その後、自分でwebサービスを立ち上げようとしたり色々していたのですがうまくいかず、今は大学に戻りつつ、低レイヤと機械学習を中心に勉強したりしています. webサービスがうまくいかなかった話はおいおい書く気になったら書こうかな.
はじめてソフトウェアエンジニアリングに触れてからそろそろ2年くらいが経ちますが、自分の実力不足の認識が深まるばかりです. 頑張らないと.
最近は機械学習の論文のサーベイをしているので、まずはそれに関する記事が続くと思います.
進捗出していきたい.